Current ongoing research at Cornell University



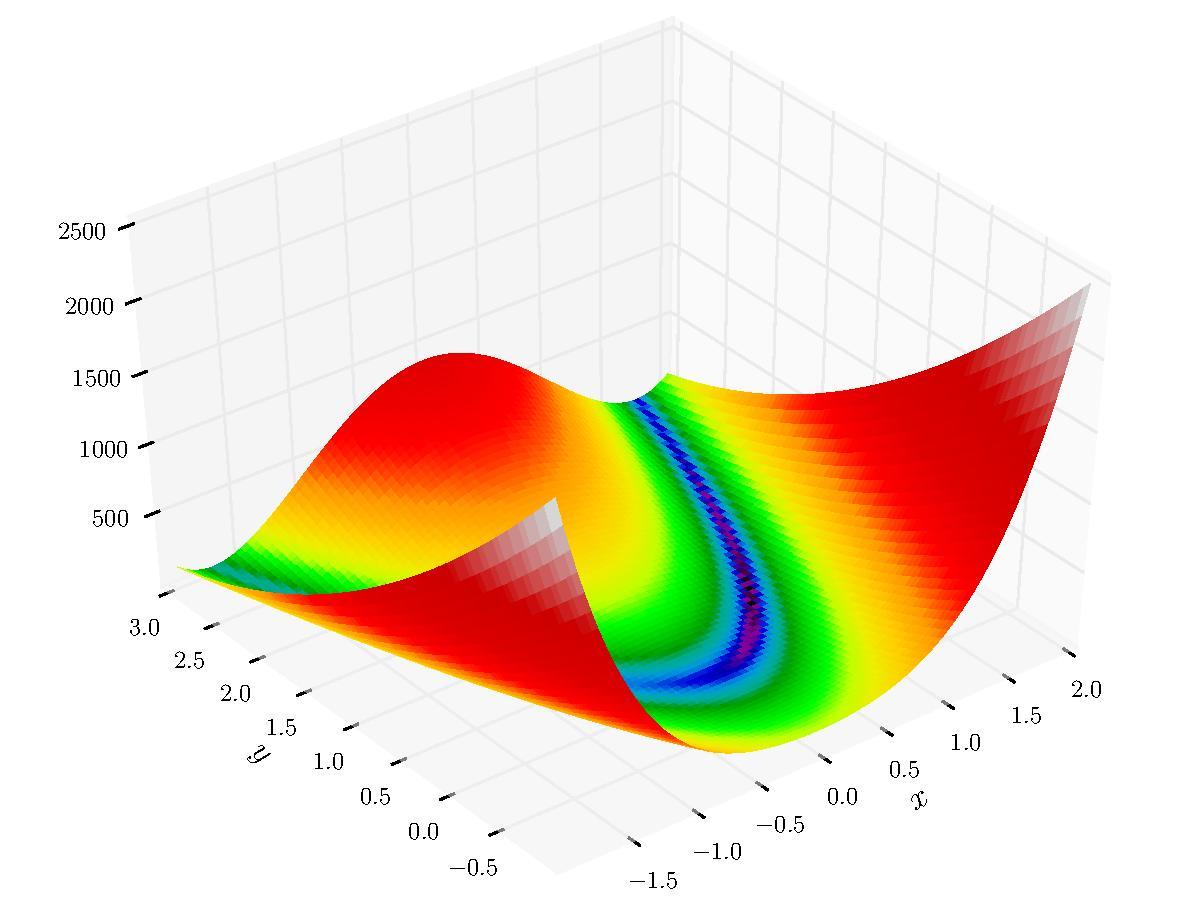
Asynchrony and elasticity in surrogate optimization

I work with Professor David Bindel and Professor Christine Shoemaker on surrogate optimization. We are working on optimization of expensive black-box functions in high-dimensions when the number of evaluations are limited. The underlying objective function is approximated by a surrogate surface (interpolating surface) and we use the surrogate surface to decide where to evaluate next.The surrogate surface can for example be a weighted sum of radial basis functions with an appropriately chosen tail function.



Software packages

Professor David Bindel and I have implemented pySOT (https://github.com/dme65/pySOT), which is an asynchronous parallel surrogate optimization toolbox written in Python. pySOT has been downloaded over 18,000 times from PyPi and has been used by many research groups. I have also implemented SOT, which is a C++11 library for surrogate optimization (https://github.com/dme65/SOT)



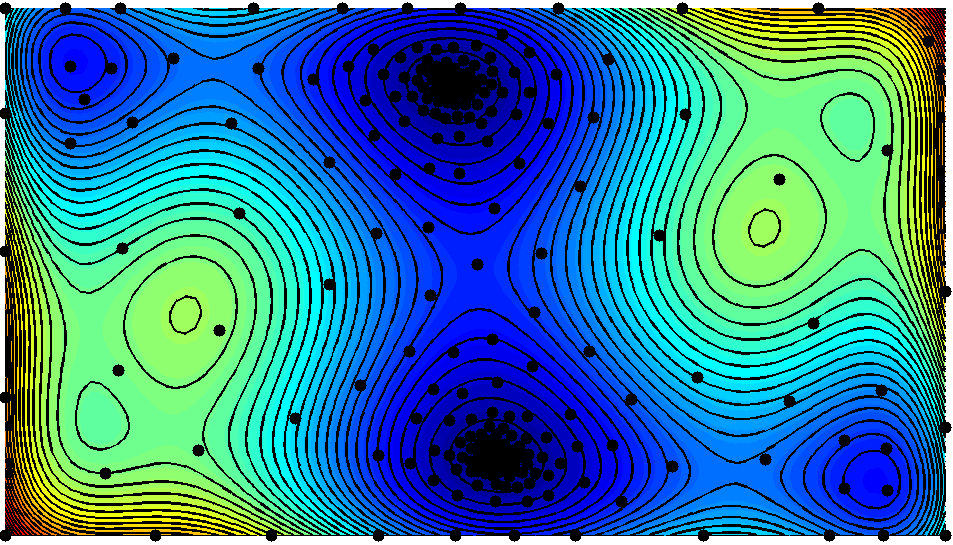
Global optimization with additional information

I work with Professor David Bindel on global optimization algorithms with provable convergence rates. We're mainly interested in designing efficient optimization algorithms given information about the semi-norm of the objective function in the native space of a given radial basis function.


$$(A*B)\,x = d$$ $$A*B := (A_{ij} \otimes B_{ij})_{ij}$$

Structured solvers

I work with Professor Charles Van Loan and Professor Alex Townsend on structured matrix problems. We're interested in problems with Kronecker product structure, such as Khatri-Rao systems of equations, where it's possible to design fast solvers that make use of the given structure.



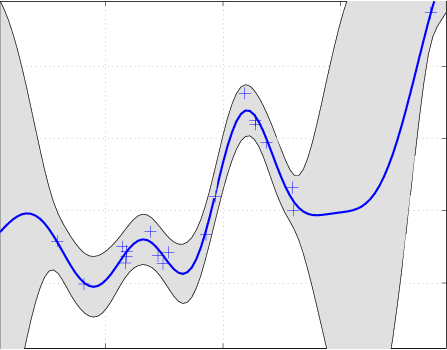
Scalable structure exploiting inference methods

I work with Professor David Bindel, Professor Andrew Wilson, and Kun Dong on scalable inference for Machine Learning. The log marginal likelihood under a Gaussian process is given by

$$\begin{align} \log p(y|X) = &-\frac{1}{2}y^T\alpha \\ &-\frac{1}{2}\log |K + \sigma^2 I| \\ &-\frac{n}{2}\log 2\pi \end{align}$$
where $K_{ij} = k(x_i, x_j)$ is the kernel matrix and $\alpha = (K + \sigma^2 I)^{-1}y$. Optimizing over the log marginal likelihood is expensive, since the standard way of evaluating $\log |K + \sigma^2 I|$ exactly involves computing the Cholesky factorization of $K + \sigma^2 I$, making each iteration $\mathcal{O}(n^3)$. This is too expensive for scalable inference methods with billions of data points, so we are interested in cheap but robust approximation schemes.