On the compressibility of tensors
SIAM J. Matrix Anal. Appl., 42(1), 275–298.

I work with Alex Townsend on compressible tensors. We explore methodologies, including smoothness of generating functions and displacement structure, that guarantee tensor compressibility. We also derive bounds on the numerical tensor ranks and storage costs in different low rank formats. Using the bounds and low rank tensor representations, we design super fast numerical algorithms to spectrally solve multidimensional Poisson equations.

Spectral, tensor, and domain decomposition methods for fractional PDEs
Comput. Methods Appl. Math., 2022.

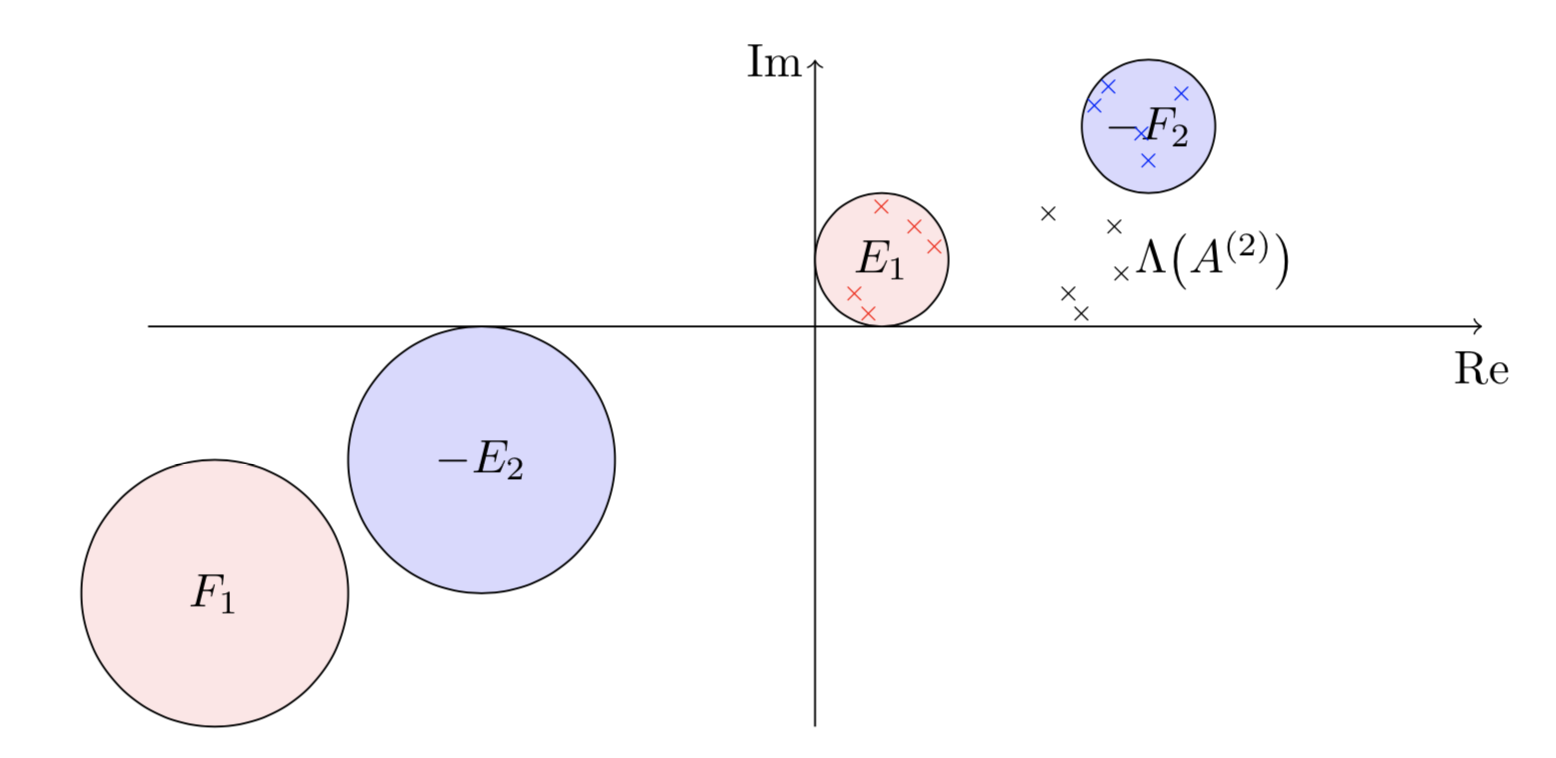
I work with Harbir Antil, and Drew Kouri, on solving fractional PDEs. We spectrally discretize extended fractional Laplacians on cubes and cylinders into tensor equations. We also incorporate domain decomposition methods to obtain multi-thread algorithms, and apply the solvers in PDE-constrained optimization.

Parallel algorithms for computing the tensor-train decomposition
Submitted to SIAM J. Sci. Compute..

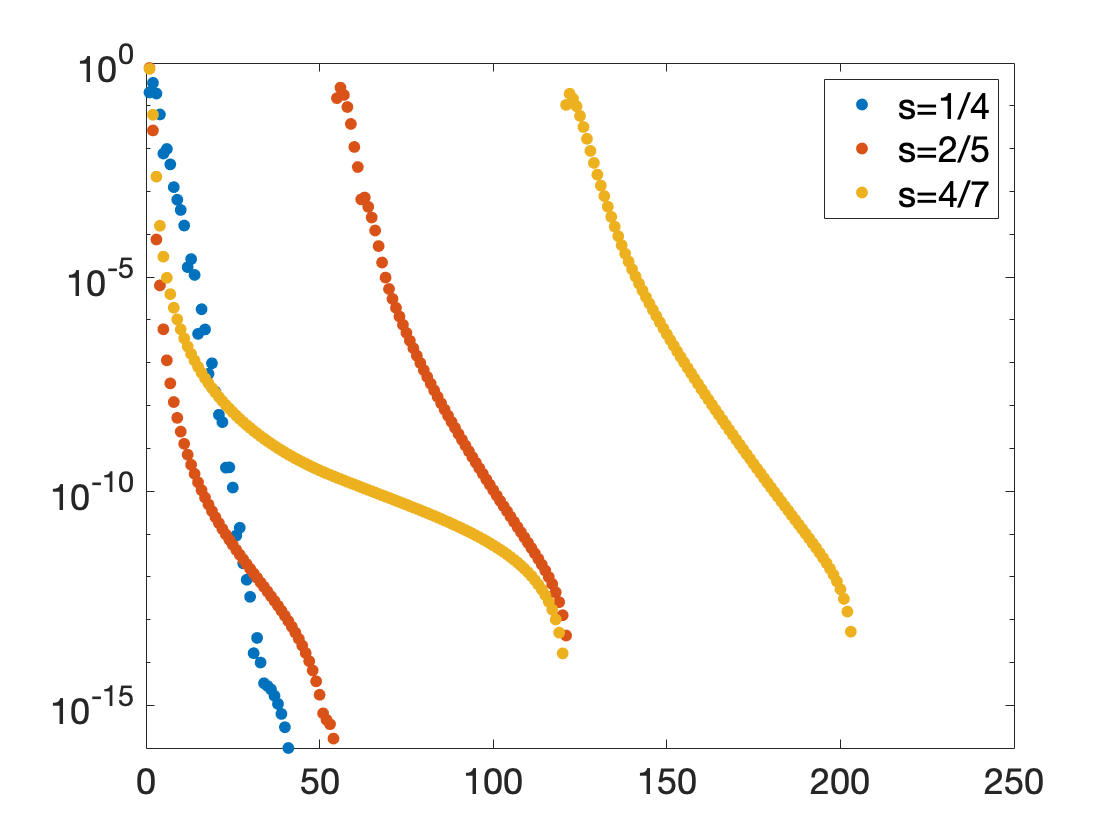
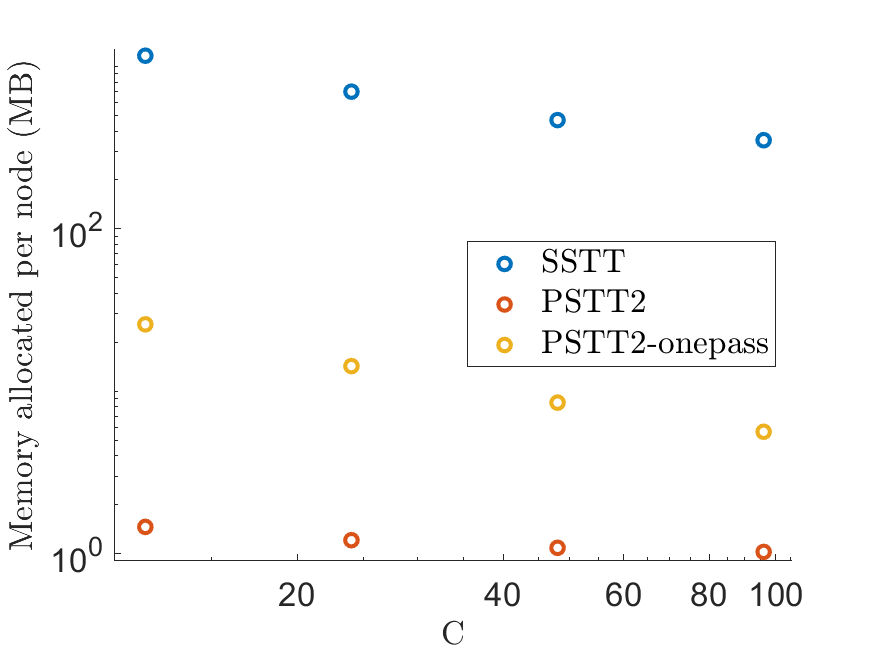
I work with Alex Townsend and Max Ruth on designing parallelizable tensor-train decomposition algorithms. Our algorithms stem from the observation that orthonormal bases of column spaces of all tensor unfoldings are connected. We propose different algorithms for various input formats, such as the whole tensor, streaming data, Tucker format, and algebraic relations. Scaling results show that our algorithms excel in both computational and storage efficiency.

Learning Green's functions associated with parabolic partial differential equations
Submitted to J. Mach. Learn. Res..

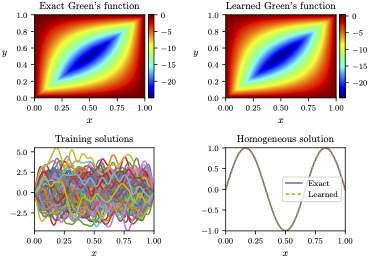
I work with Nicolas Boullé, Seick Kim, and Alex Townsend on learning Green's functions of 1D parabolic PDEs. We show that the Green's functions have a hierarchical off-diagonal low rank structure, and learn the low rank domains with randomized linear algebra. In practice, we can use neural networks to replace randomized input and output pairs, and numerical tests illustrate the strength and efficiency of our scheme.

Tensor equation methods to compute electron correlation energy

I work with Sherry Li and Yang Liu on computing electron correlation energy in computational chemistry. We discover the underlying structure of the original linear system, and rewrite it into a Sylvester tensor equation. Depending on different chemical orbitals chosen, we design different direct and iterative low rank algorithms. Numerical tests on chemical data indicates that our methods are more efficient than traditional linear system solvers, and can handle much larger problems.